EIA Predicted¶
The EIA releases an annual energy outlook, with projections of the energy landscape into the middle of the century. The EIA’s annual energy outlook in 2013 was to the year 2040, but we will keep with our 22 year outlook to 2035 to compare with Brian’s Austere Agenda.
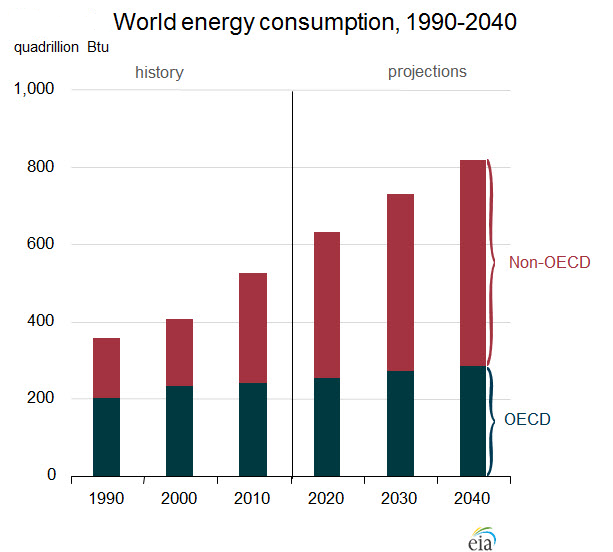
According to the EIA study, realistic projections for 2035 are around 790 quadrillion BTUs, where the Organization for Economic Co-operation and Development (OECD) countries are distinguished from non-OECD countries. EIA also projects the total energy consumption in the US by 2035 to be around 105 quadrillion BTUs. So this means that the average global citizen will consume on average 3.5 kW, or
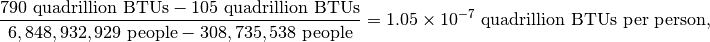
which is equivalent to

In contrast, the EIA predicts the average US resident will consume about 5% more energy than they do at present, or on average 11.4 kW in 2035. This pulls the average world citizen to 31% of the average US citizen. What this also means is that well into the 21st century the average world citizen will be consuming about 33% that of what an average US citizen was able to consume in four years ago in 2010.

This projection, by resource, breaks down to about 225 quadrillion BTUs of liquid fuels (such as petroleum), 175 quadrillion BTUs of natural gas, 220 quadrillion BTUs of coal, and 110 quadrillion BTUs of renewables, and about 60 quadrillion BTUs of nuclear. That’s about 28% petroleum, 22% natural gas, 28% coal, 14% renewables and 8% nuclear power.
This amounts to about a 2.7 fold increase in renewable energy resources in 22 years, an addition of only about 69 quadrillion BTUs of new energy. This also indicates a mere 1.8 fold increase in nuclear, or 26 quadrillion BTUs of new energy from nuclear.
What does this mean logistically? For nuclear fission reactors, this means the production of somewhere between 500 and 800 new reactors in the next 22 years, since
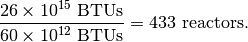
At present about 60 reactors are planned to be completed by around 2020. So clearly the EIA is being very optimistic about a coming sea change in nuclear energy policy.
As far as the 69 quadrillion BTUs coming from renewables, on the international stage this means almost 80 percent of the projected increase in renewable electricity generation is fueled by hydropower and wind power, while in the US almost 80 percent of the EIA projected increase in renewable electricity generation is fueled by wind power and biomass. The only realistic way of creating this much hydroelectric power, as we discussed above, is to use hydroelectric dams. Getting this much energy from tidal wave plants would require building about 80,000 of them, which would cover an outrageous ocean area of around 2 million  .
.
The major problem is hydroelectric dams only make sense in areas that have rivers with very high volumetric discharge. Dams then represent a patchwork solution, since you rapidly reach an upper bound, after which all of these river resources have been tapped, and hydroelectricity power generation cannot easily be extended any further.
Recovering an additional 69 quadrillion BTUs from wind energy is unrealistic for the same reasons as tidal power generation, and this is also recognized ny the EIA that shows that the vast majority of this energy is assumed to be coming from hydroelectric dams.
Perhaps the saddest observation, is this energy could much more easily be obtained from nuclear fission plants (with a substabtially smaller environmental footprint), as nuclear fission is so much more energy dense than hydroelectric. In that scenario you could reach this goal by creating
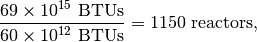
nuclear reactors, or a reasonable 50 every year for the next 22 years. But since world energy policy is in a residing state of potent and perpetual confusion, this seems unlikely.
