Brian’s Austere Agenda¶
“Brian’s Austere Agenda” is based on the sub-optimal future invisioned by Brian Cox that wishes to meet the goal of providing half the energy consumed by the average US citizen today (as of the year 2010) to the average world citizen in the year 2035. So that means that the average global citizen would be able to on average consume 5.3 kW per person by the year 2035. So working within the constraint of constant US energy consumption, and that world and US populations also remain constant, we can calculate the non-US global average energy consumption per person, which is simply 2.1 kW per person, or
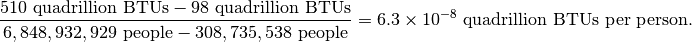
These number are found at the US census, where the population clock can be of use. To convert energy in BTUs to power in watts, you have to compute the following:
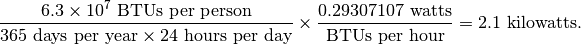
So to meet Brian’s Agenda we need to raise that 2.1 kW per person to 5.3 kW per person, which is a 2.5 fold increase on avergave in energy consumed per (non-US) person. That means the total amount of energy needed to reach this goal is 1278 quadrillion BTUs.
Let us assume the optimistic assumption that peak petroleum production reaches 150% of its current capacity, or 263 quadrillion BTUs per year, making up about 21% of the needed energy. Assuming the same for peak natural gas to 176 quadrillion BTUs or 14% of the needed energy, and the same for peak coal to 221 quadrillion BTUs, or 17% of the needed energy. In total this yields 52% of the needed energy, leaving the remaining 618 quadrillion BTUs to non-fossil fuels. As we will see below, these numbers are slgihtly higher than even the most idealized projections of the EIA, but we will use them here to avoid subtleties that have very little impact on the larger picture.
From what remains, 41 quadrillion BTUs are consumed from renewable sources and 34 quadrillion BTUs come from nuclear fission. That means, in order to meet the Brian agenda of each person on the planet living on half as much energy as the average US citizen by 2035, we need to somehow in the next 22 years produce 543 quadrillion BTUs from either enhanced renewables or nuclear (or, perhaps, some visionary new energy approach?).
Okay, so how can we possibly more than double the energy production of the world in 22 years entirely from renewables and/or nuclear fission? One way would be to provide this energy entirely from one type of energy resource. Conventional wisdom supports the idea that “all of the above” is the way to go. Presumably this would mean that some mixture of renewables and nuclear would be the most effective way of achieving our energy need of 543 quadrillion BTUs (since we have already squeezed way more from fossil fuels than we percieve to be possible). So let’s take a look at these options.
Since we have developed some sense of what energy density is above, it is obvious that the most efficient way of reaching our goal (most efficient in the sense of “most energy per unit mass or volume”) would be to use soley the most energy dense solution, which in our case is clearly nuclear fission (by many orders of magnitude).
So what would it mean to produce 543 quadrillion BTUs of energy in 22 years using nuclear fission plants? Let’s again be overly optimistic, and assume that each nuclear energy plant produces a usuable 2 GW (Gigagwatt) of power, which correpsonds to 2 GW  h of energy, or 6.8 billion BTUs each (this is almost twice as much power as the largest reactors in existence today provide). Multiplying by the 24 hours in a day and the 365 days in a year, that means each reactor produces about 60 trillion BTUs per year, which sounds like a lot.
h of energy, or 6.8 billion BTUs each (this is almost twice as much power as the largest reactors in existence today provide). Multiplying by the 24 hours in a day and the 365 days in a year, that means each reactor produces about 60 trillion BTUs per year, which sounds like a lot.
So how many fission reactors would we need to reach our goal of 543 quadrillion BTUs? To calculate this, all we have to do is divide the total energy needed by the energy produced by one reactor, in other words:
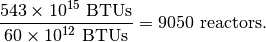
Okay, so we need to build 9050 reactors in 22 years. That works out to 1.13 reactors per day, everyday, needing to built to reach this goal. At present there are about 437 nulcear power plants in the world (built over 50 years) and 68 currently under construction. So we would need to increase our nuclear fission production rate by about 4700%.
So that seems a little bit far-fetched, as that would require an immediate and frenzied world effort to expand a rather small industrial infrastructure, into a churning worldwide nuclear fission industry in a matter of days. Let’s see how well the next lowest energy density renewable scales.
As it turns out, the second highest energy density renewable is solid biomass/biofuels, though this is somewhat misleading. The reason is, much of this energy is derived from the environmentally carbon-nonneutral burning of wood or biomass, and as a consequence can be seen as a sort of quasi-renewable energy source. This is because if consumption surpasses production, these can disappear completely (i.e. deforestation, etc., the “mass” must have sufficient time to “replenish” or “grow”).
To put some things in perspective, let’s take this opportunity to look at the effecitve energy density fall-off between our two ‘best’ options here. Nuclear fission has an energy density of 83,140,000 MJ/kg, while wood has an energy desnity of about 20 MJ/kg. Looks pretty scary, but nuclear fission plants are actually still (due to lack of research, presumably) incredibly innefficient at extracting the energy they contain. So things aren’t quite as bad as they seem.
The largest biomess-fuled power plants in the world produce less than 300 MW of power, for example the Alholmens Kraft Power Station in Finland. That’s an energy production of 300 MW  h of energy. Well, we can see where this is going right off, just by looking at our fission reactors. These thermal biomass reactors produce less than 1/6th the energy of a fission reactor. So what this means is now, instead of needing to build 9050 fission reactors in 22 years, we would need to build more like 60,334 biomass thermal reactors in 22 years. In addition to running out of fuel/forests, this would mean that we would need to build about 7.5 reactors a day for 22 years, which would also be a whole lot of carbon non-neutral exhaust.
h of energy. Well, we can see where this is going right off, just by looking at our fission reactors. These thermal biomass reactors produce less than 1/6th the energy of a fission reactor. So what this means is now, instead of needing to build 9050 fission reactors in 22 years, we would need to build more like 60,334 biomass thermal reactors in 22 years. In addition to running out of fuel/forests, this would mean that we would need to build about 7.5 reactors a day for 22 years, which would also be a whole lot of carbon non-neutral exhaust.
So that’s quite extreme. Let’s move to what the public seems to view as more environmentally friendly options, which it turns out are also substantially less energy dense. So, what about solar? Solar energy cells currently have an energy density of about 175  . Let’s assume we can triple these energy densities (this is extremely optimistic, probably well into the realm of unrealistically optimistic). Then we can say we have solar cells with an energy density of about 525
. Let’s assume we can triple these energy densities (this is extremely optimistic, probably well into the realm of unrealistically optimistic). Then we can say we have solar cells with an energy density of about 525 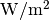 .
.
To see this, observe the current research cell efficiencies as reviewed by the National Renewable Energy Laboratory (NREL). On the higher end, these cells are so expensive per unit area, as to be completely non-commercializable, and we assume a solar cell of 60% efficiency (which is 19% higher than even the most expensive experimental cells in existence today). Now, solar panels can only produce energy part of the day, depending on the light intensity. If you count this up, you get about 8 hours a day of actual energy production. So that’s about 4.2 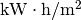 per day, or about 14.3 thousand
per day, or about 14.3 thousand 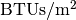 per day, or about 5.2 million
per day, or about 5.2 million 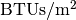 per year. So that means that to reach our goal of 543 quadrillion BTUs, we would need:
per year. So that means that to reach our goal of 543 quadrillion BTUs, we would need:
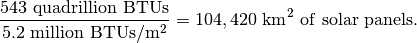
That means we need to produce about 15.1 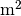 of solar panels every second for 22 straight years. In other words, this means we would need to produce about 13
of solar panels every second for 22 straight years. In other words, this means we would need to produce about 13 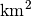 of solar panels per day, or, equivalently, that’s covering 2431 football fields worth of land in solar panels every day for the next 22 years (a total land area twice the size of Texas).
of solar panels per day, or, equivalently, that’s covering 2431 football fields worth of land in solar panels every day for the next 22 years (a total land area twice the size of Texas).
Next let’s consider hydroelectric power plants. The largest hydroelectric power plant (in fact largest power producing facility) in the world is Three Gorges Dam in China, that produces a remarkable 9.85 TW  h of energy per year. So that’s 98,500 GW
h of energy per year. So that’s 98,500 GW  h per year, or 335 trillion BTUs per year. To reach our goal of 543 quadrillion BTUs, that would require building only 1621 of these plants in the next 22 years, or about one every four days. So what’s the problem? Well, the Three Gorges Dam is located on the Yangtze river, the third longest river in the world and the sixth largest river in the world by volumetric discharge. To put this in perspective, The 14th largest river in the world by volumetric discharge has less than half the volumtric discharge of the Yangtze. It should also be noted that the Three Gorges Dam is one of the largest artificial structures in the world with a height of 594 ft, and a length 7,661 ft. (over one mile across), and it took about 14 years to build. So we only would need 1752 of them (that’s about 80 of these per year), and somehow find the rivers to put them all on as well. In addition, dams of this size tend to be quite environmentally controversial.
h per year, or 335 trillion BTUs per year. To reach our goal of 543 quadrillion BTUs, that would require building only 1621 of these plants in the next 22 years, or about one every four days. So what’s the problem? Well, the Three Gorges Dam is located on the Yangtze river, the third longest river in the world and the sixth largest river in the world by volumetric discharge. To put this in perspective, The 14th largest river in the world by volumetric discharge has less than half the volumtric discharge of the Yangtze. It should also be noted that the Three Gorges Dam is one of the largest artificial structures in the world with a height of 594 ft, and a length 7,661 ft. (over one mile across), and it took about 14 years to build. So we only would need 1752 of them (that’s about 80 of these per year), and somehow find the rivers to put them all on as well. In addition, dams of this size tend to be quite environmentally controversial.
That being said, another interesting idea that has generated some interest in hydroelectric energy is that of wave energy, or tidal power plants. The largest tidal power plant in the world right now is the Sihwa Lake Tidal Power Station in South Korea. This plant produces about 254 MW  h of energy, or 863 billion BTUs. That means we would need to build more that 629,000 of these plants in the next 22 years to reach our goal. That’s producing about 78 tidal plants per day. It should also be noted that the tidal basin for the Sihwa Power Station has an area on the ocean floor of about 30
h of energy, or 863 billion BTUs. That means we would need to build more that 629,000 of these plants in the next 22 years to reach our goal. That’s producing about 78 tidal plants per day. It should also be noted that the tidal basin for the Sihwa Power Station has an area on the ocean floor of about 30 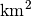 . So if we build 629,000 of them, that’s more than 18 Million
. So if we build 629,000 of them, that’s more than 18 Million 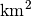 , or 3.5 billion football fields covering the ocean floor. The area of the surface of the ocean is 361 million
, or 3.5 billion football fields covering the ocean floor. The area of the surface of the ocean is 361 million 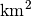 , so this would be equivalent to covering the entire surface of the world’s oceans tens times over in order to meet this energy demand.
, so this would be equivalent to covering the entire surface of the world’s oceans tens times over in order to meet this energy demand.
Of course, in truth, tidal power plants have relatively low conversion efficiency leading to an actual energy density of around 4 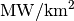 , which works out to about half the energy of what we have just calculated above. So taking energy conversion efficiency into account (and assuming it can raise to around 50% efficiency), we would need to build around 1.2 million tidal generators in the next 22 years, and cover the world’s oceans twenty times over with them in order to meet our energy demand.
, which works out to about half the energy of what we have just calculated above. So taking energy conversion efficiency into account (and assuming it can raise to around 50% efficiency), we would need to build around 1.2 million tidal generators in the next 22 years, and cover the world’s oceans twenty times over with them in order to meet our energy demand.
What about wind turbines? Wind turbines it turns out have similar energy density to tidal generators. The largest wind farm in the world is the Alta Wind Energy Center in California. It produces about 1.3 MW  h of power, which is 0.5% of the energy produced by the Sihwa Lake Tidal Power Station in South Korea, while still requiring about 30
h of power, which is 0.5% of the energy produced by the Sihwa Lake Tidal Power Station in South Korea, while still requiring about 30 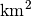 of land. So that means we would need to build about 126 million wind farms in the next 22 years (or about 16,000 wind farms per day), and cover the surface of the earth (all the land and all the oceans) tens times over. Seems tricky.
of land. So that means we would need to build about 126 million wind farms in the next 22 years (or about 16,000 wind farms per day), and cover the surface of the earth (all the land and all the oceans) tens times over. Seems tricky.
Finally, let’s consider the other environmentally carbon-nonneutral form of biofuel, such as bioalcohols and so-called advanced bio-fuels from biomass, etc. Most types of biomass have lower energy density than coal (which has about half the energy density of gasoline), though it’s not the energy density of biomass that is the primary limiting factor. For advanced biofuels, the biomass must be produced in enormously large quantities for use. For example, if we make the optimistic assumption that the form of biomass we want is for thermal conversion, and has half the energy density of coal, then we would need to produce from scratch 7.4 times as much biomass as there was coal mined in 2010, by weight. So since there was 146.653 quadrillion BTUs from coal in 2010, that works out to about 10.6 billion tonnes of coal. So we would need to produce 39.2 billion tonnes of biomass to meet our goal of 543 quadrillion BTUs of energy. The density of biomass varies, but is usually at least 10 times less than coal (making it very difficult to transport), meaning we would need about 392 billion litres of biomass, or about 156,800 olympic sized swimming pools of biomass in 22 years time, which is about 20 olympic sized swimming pools of biomass per day, every day, for 22 years. For perspective, that is over a thousand times the total weight of all the potatoes produced in the world in 2011. In fact, if you sum together the top twenty world crops by weight, reaching this goal would require producing about 2.6 times that amount per year just to burn in biofuel reactors, for 22 years straight.
In summary, as the most energy dense option (nuclear fission) is essentially unnattainable, any mixture of the above is that much worse. Thus, from the Brian agenda point of view, the “all of the above” approach to solving the energy needs of our future, seems to lack both in understanding as well as focus. The synopsis being: unless we find a substantially more energy dense solution, Brian’s austere agenda is completely impossible to reach.
